La inclusión de la neurociencia y los avances en las técnicas de neuroimagen han dado las claves para saber qué zonas cerebrales se activan en los procesos matemáticos. Podemos saber qué ocurre en el cerebro cuando realizamos una operación o resolvemos un problema. Y conocer todo esto es indispensable para tener una buena praxis de la materia. Sin embargo, y a pesar de los avances, los procesos de enseñanza han cambiado muy poco a lo largo de los años.

Por tanto, es completamente crucial, que se establezcan dos líneas a trabajar desde el punto de vista de la docencia; por un lado, conocer los procesos mentales de las matemáticas, en tanto en cuanto esto repercutirá en la ejecución de los aprendizajes concretos (aprender a sumar, dividir, resolver un problema, de manera eficiente), y, por otro, analizar y cuestionar el modelo de enseñanza general de la materia.

¿Qué son las matemáticas?

Según Sfard (1991), aprender matemáticas implica un esfuerzo continuo que incluye procesos cerebrales simples como atención, memoria, o procesos mentales más complejos como la organización de ideas, la comparación, el análisis, el razonamiento, seguir pasos, cumplir reglas y realizar toma de decisiones. Por tanto, es un proceso tan complejo que no se puede reducir a la aplicación de algoritmos memorizados para operar o a la resolución sistemática de problemas.

Ya Piaget (1969), en su revisión teórica, determinó las bases de las nociones lógico-matemáticas, estructuradas desde etapas tempranas, cuando el niño interactúa con los objetos que hay en su medioambiente, y, por tanto, podemos decir que son innatas al ser humano. El niño comienza a procesar las matemáticas a través de la memoria visual y la retención de imágenes (estado sensoriomotor); después a través del movimiento y la interacción con el entorno (estado preoperacional) y, por último, con el uso del lenguaje (estados operacionales), herramienta imprescindible para la adquisición del sistema simbólico.

Etapa sensoriomotora (0-2 años)
Estadio prelingüístico, apoyado en los movimientos y en la percepción. Estudios como el de Wood y Spelke, (2005) muestran evidencias de que los bebés de pocos meses ya desarrollan conceptos sobre operaciones y estimaciones, basadas, además, en la memoria visual y con relación al tiempo de exposición de los objetos. Algunos estudios muestran la reacción de niños menores de un año ante la “desaparición” de objetos: se les enseña un juguete y se oculta tras una pantalla, se repite la operación con un segundo objeto. Al quitar la pantalla, sólo hay un juguete y la reacción del niño es de observación prolongada sobre este, como si estuviera esperando, lógicamente, que aparecieran dos objetos y no uno. Esto se interpreta como una capacidad innata de pensamiento matemático (Vargas, 2013).

Etapa preoperacional (2-7 años).
Se inicia la utilización de símbolos y el desarrollo de la habilidad para solicitar cosas que no están presentes. Sin embargo, su pensamiento se centra en situaciones del momento que vive y la adquisición de los conceptos matemáticos simbólicos se establecen mediante un vínculo con su propio cuerpo; tal es el caso del uso de los dedos para contar, como determinan Fischer y Brugger (2011).

Estas dos primeras etapas, por su carácter perceptivo, determinan unas matemáticas más innatas, relacionadas con el sentido numérico. Para comprender los números, se adquiere primero el concepto de cantidad, los niños saben que hay diferencias si ven uno o dos objetos, independientemente de que se represente con un símbolo (1 ó 2).

El concepto de número es una representación mental de una cantidad y, por tanto, está íntimamente ligado a la espacialidad. Primero, por su relación entre lo que vemos en nuestro entorno (cantidad de objetos) y su representación mental (número simbólico), y, segundo, por el sistema numérico que hemos adquirido, dando valor a las cifras por su valor posicional. Un 5 no tiene el mismo valor en 59 que en 543. Por tanto, si el niño no ha desarrollado un desarrollo espacial suficiente, no podrá adquirir el concepto número de manera correcta. Este proceso se produce en torno a los 7 años, con el afianzamiento de la lateralidad. Las actividades que se hacen antes de esa edad deben ir orientadas a fomentar ese desarrollo lateral y a motivar el cálculo estimado, que será lo que permita la adquisición del concepto cantidad, y no tanto a resolver operaciones de manera abstracta, ya que puede hacer que no se asienten las bases de manera correcta y arrastrar problemas en la adquisición de las matemáticas a lo largo de toda la vida.

Las habilidades matemáticas innatas son:

Numerosidad: habilidad de determinar, sin necesidad de contar, un grupo de tres o cuatro elementos.
Ordinalidad: capacidad para detectar qué conjunto es mayor o menor en número, en grupos de dos, tres o cuatro elementos.
Cálculo: habilidad para numerar y contar pequeños grupos de elementos mediante un sistema no verbal.
Aritmética: habilidad para detectar pequeños incrementos o decrementos en la cantidad de un conjunto de pocos elementos.
Estimación: valoración de cantidades, magnitudes y tamaños relativos.
Geometría: comprensión de la forma y las relaciones espaciales.

No obstante, esto resulta insuficiente; para desarrollar unas capacidades matemáticas más complejas, se debe incorporar el conteo verbal, esto es, la habilidad para el recuento consciente y con significado. Tanto las capacidades innatas numéricas como las derivadas de la adquisición del lenguaje (en las etapas operacionales) son imprescindibles y conforman un proceso iterativo. Aprender a contar implica rastrear las magnitudes pre-verbales, innatas, en relación a los símbolos numéricos verbales y escritos, adquiridos; así como el proceso inverso que determina la relación entre los símbolos numéricos y las magnitudes pre-verbales (Gallistel y Gelman, 1992).

Por tanto, con la adquisición del lenguaje, en su concepto más amplio, se desarrollan habilidades suficientes para poder establecer reglas, estructurar procesos y abstraer el código numérico.

Etapa de las operaciones concretas (7-12 años)
El niño realiza operaciones lógicas y es capaz de color objetos y sucesos en un orden determinado, comprende la noción de peso, volumen, distancia, etc. A pesar de eso, su pensamiento sigue centrado en cosas concretas del mundo que le rodea.

Etapa de las operaciones formales (12-14 años)
Se llega a la abstracción de las matemáticas, al pensamiento simbólico. Su pensamiento no se centra solo en situaciones concretas presentes y aparece el razonamiento hipotético-deductivo.

A medida que se va pasando de un estadio a otro, la importancia del lenguaje aumenta, y es en las etapas operacional concreta y operacional formal, donde toma mayor preponderancia sobre otros aspectos de las matemáticas.  Estudios neuropsicológicos determinan la doble disociación del cerebro en la manera en la que se enfrenta a la aritmética y, así, pacientes con lesiones cerebrales que no recordaban las tablas de multiplicar, podían llevar a cabo resolución de problemas de multiplicación, y, contrariamente, paciente que, aun habiendo perdido muchas habilidades matemáticas, podían enumerar las tablas de multiplicar (Cánovas, 2009).

Estas relaciones numéricas entre lo innato y lo adquirido se establecen mediante esquemas aprendidos, que Resnick (1989) definió como esquemas protocuantitativos:

Esquema de comparación: expresión verbal, sin componente numérico, de cantidades, tamaños y magnitudes. Por ejemplo: “más, menos”.
Esquema de incremento-decremento: capacidad de determinar si se ha añadido o sustraído algún elemento al conjunto, independientemente de la distribución espacial.
Esquema de parte-todo: saber distinguir entre la parcialidad y el total y comprender que una forma parte de la otra.

Por tanto, las capacidades numéricas innatas del ser humano evolucionan con el lenguaje hacia el conteo, que, a su vez, se integra con los esquemas protocuantitativos para desarrollar la capacidad de enfrentarse a la resolución de situaciones reales.

¿Qué ocurre en nuestro cerebro cuando hacemos matemáticas?

De los procesos seguidos en la evolución del concepto numérico innato al desarrollo de esquemas establecidos, se determinan las áreas cerebrales involucradas en los procesos matemáticos. Como se anticipaba, el razonamiento matemático lleva adscritos procesos de atención, memoria, análisis, planificación, organización, etc.  Y esto se traduce en una actividad cerebral compleja y holística, donde todos los lóbulos del encéfalo son necesarios de una u otra manera, además de una participación activa de ambos hemisferios.

Debido a la «espacialidad» de los números, la región que más se activa es el lóbulo parietal. Dependiendo de la habilidad matemática empleada, se activarán unos circuitos u otros.

Cálculo estimado. También llamado cálculo aproximado, es el primero que se desarrolla, de manera innata. En este proceso se activa el segmento horizontal del surco intraparietal, es decir, la parte más profunda del lóbulo parietal, relacionado con el procesamiento visual y espacial, donde se desarrolla el sistema cuantitativo no verbal.

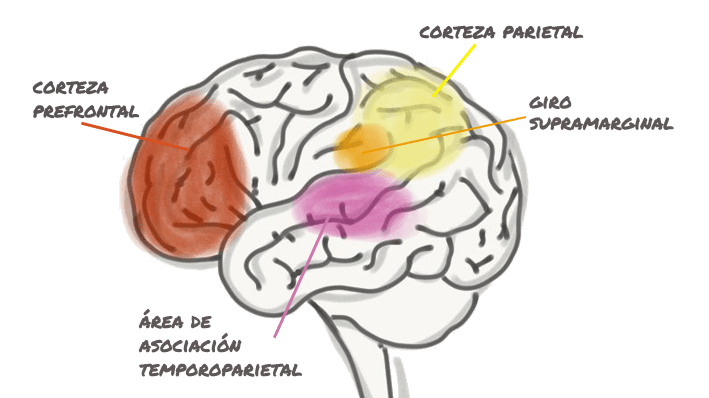
Cálculo aritmético exacto. Supone integrar la capacidad espacial y el lenguaje, por tanto se activan áreas como la corteza parietal posterior bilateral (espacio y cantidad); el giro supramarginal, en estrecha relación con el área de Wernicke (almacén fonológico o de las palabras), y las áreas de asociación parieto-occipito-temporal, donde se registran los estímulos visuales (occipital), espaciales (parietal) y se codifican con lo almacenado en la memoria (temporal). Para calcular 3 + 2 debemos recordar que 3 se refiere a la cantidad de un objeto, otro y otro, y, además, recordar que el signo + implica añadir o juntar.

Resolución de problemas. Además de los lóbulos parietales y las áreas de asociación parieto-occipito-temporal necesarias para el cálculo, es importante destacar la función que realiza la corteza prefrontal bilateral, relacionada con las funciones ejecutivas, es decir, planificar, analizar, organizar, razonar, etc.

¿Cómo debemos enseñar las matemáticas?

Sabiendo cómo funciona el cerebro, así como las edades a las que madurativamente está preparado para según qué destreza, podremos establecer una metodología óptima de acuerdo a las capacidades cognitivas de los alumnos, evitando situaciones ineficaces o problemas futuros. Además, entender el proceso evolutivo de las matemáticas es muy útil para mejorar las destrezas que no se hayan adquirido correctamente.

Por ejemplo, si nos encontramos con un/a niño/a que no es capaz de calcular bien, debemos analizar si el problema está en su memoria (no recuerda las reglas), en su concepción del número (no tiene bien adquirida el valor posicional) o incluso si su cerebro, madurativamente hablando, aún no está preparado para ello (no tiene definida la lateralidad). Por tanto, el trabajo que hay que hacer variar;, de nada sirve hacer operaciones una y otra vez para practicar, si no es capaz de entender el concepto del número.

Este análisis del proceso hay que hacerlo sea cual sea la edad de los/as alumnos/as, pues no podemos dar por hecho que en las etapas anteriores se haya adquirido correctamente. A menudo, el aprendizaje de las matemáticas se ha centrado en trabajar el cálculo exacto, desarrollando el pensamiento convergente, sin apenas pasar por la estimación de cantidades o el fomento de un pensamiento más divergente y flexible, y esto dificulta el proceso mental necesario, por lo que retomar esta actividad es fundamental para ser eficaz en el proceso de enseñanza-aprendizaje, a cualquier edad.

De todo esto se deducen los puntos clave a trabajar en el área de matemática:

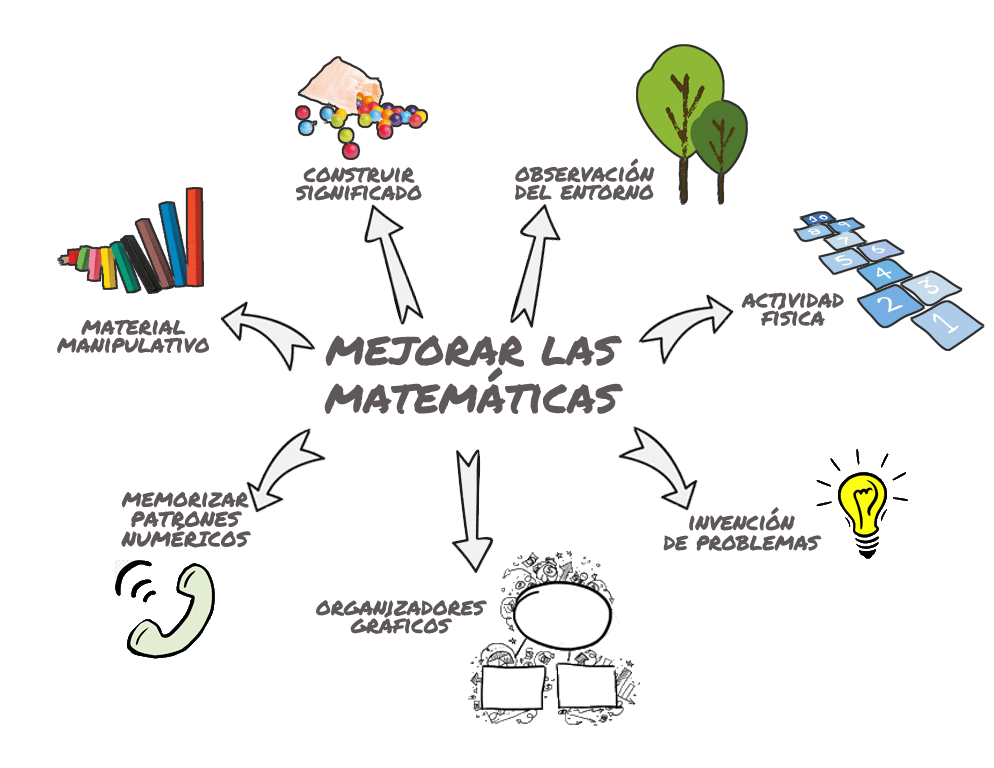
AUMENTAR LOS PROCESOS PERCEPTIVOS. Trabajando la recepción, codificación y registro de la información de estímulos multimodales. Es decir, cuanta más información tengamos de un mismo concepto por diferentes vías, más compleja será el registro que elaboraremos. En el caso de conceptos relacionados con la espacialidad, como es el caso de los números, o de las matemáticas en general, toma sentido trabajar la percepción táctil, ya que la información registrada de manera visoespacial ayudará a elaborar un esquema cognitvo más allá de un código simbólico. Es imprescindible trabajar con material manipulativo.

AFIANZAR LA LATERALIDAD. Esto supone la especialización hemisférica, es decir, que uno de los dos hemisferios sea el dominante (en mano, pie, ojo y oído). Esta dominancia se da cuando las conexiones entre ambos son eficientes y, por tanto, el cerebro está suficientemente maduro para terminar de entender el espacio. Para mejorar este proceso es importante realizar actividad física, sobre todo la que conlleva la coordinación de ambas partes del cuerpo, ya que esto hace que aumenten las conexiones interhemisféricas.

TRABAJAR EL CÁLCULO ESTIMADO. El proceso más básico de esto es la subitización, es decir, estimar de manera visual una cantidad, esto ayuda a mejorar la comprensión del número. Además, ayuda a agilizar el cálculo mental, ya que mejora las representaciones mentales de las cantidades. En etapas en las que el pensamiento es concreto y centrado en el entorno (hasta los 12 años), es necesario trabajar la observación y la estimación de cantidades, pues será lo que favorezca los aprendizajes abstractos futuros. Incorporar los esquemas protocuantitativos (comparación, incremento-decremento, parte-todo) de manera explícita favorecerá el cálculo estimado en etapas más complejas.

TRABAJAR EL CÁLCULO EXACTO. Cuando se tiene madurez suficiente, incorporar el cálculo exacto. La concepción de las operaciones sigue el mismo proceso que los número, por tanto, necesita una fase perceptiva, manipulativa y estimada, para finalmente incorporar el lenguaje (etapas operacionales). Hasta que no se dominan los procesos previos, no tiene sentido pasar a la abstracción del lenguaje matemático.

DESARROLLAR LA MEMORIA DE TRABAJO. Si trabajamos de manera específica esta función cognitiva, facilitaremos la adquisición de las destrezas matemáticas. Por un lado hay que fomentar la memoria numérica (con juegos donde haya que retener números por un breve tiempo) y, por otro, la procedimental, que se mejora con la estructuración explícita del proceso, por ejemplo, los pasos a seguir para dividir.

FOMENTAR LAS FUNCIONES EJECUTIVAS. Sobre todo, la planificación, que será de gran utilidad en la resolución de problemas. Por ello, es muy importante seguir una estructura clara y apoyarse en organizadores gráficos, ya que estos mejoran la imagen mental del proceso.

FAVORECER EL PENSAMIENTO DIVERGENTE. Más allá de la estructuración de los cálculos o la resolución de problemas, las matemáticas nos enfrentan a la vida real, por tanto, debemos fomentar un pensamiento divergente, flexible, muy de la mano de la estimación y, sobre todo, de la creatividad. Una buena actividad es la invención de problemas.

Bibliografía

Cánovas, D. A. (2009). Cerebro, números y educación = Brain, numbers and education. Aula. Universidad de Salamanca, 15, 79–90.
Fischer, M. H., & Brugger, P. (2011). When digits help digits: Spatial-numerical associations point to finger counting as prime example of embodied cognition. Frontiers in Psychology, 2(260).
Gallistel, C. R., & Gelman, R. (1992). Preverbal and verbal counting and computation. Cognition, 44(1–2), 43–74.
Resnick, L. B. (1989). Developing Mathematical Knowledge. American Psychologist, 44(2), 162– 169.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational Studies in Mathematics, 22(1), 1–36.
Vargas, A. R. (2013). Matemáticas y neurociencias: una aproximación al desarrollo del pensamiento matemático desde una perspectiva biológica. Revista Iberoamericana de Educación Matemática, 36, 37–46.
Wood, J. N., & Spelke, E. S. (2005). Chronometric studies of numerical cognition in five-month-old infants. Cognition, 97(1), 23–39.